Matlab技巧24：MATLAB绘制B样条曲线详解（第1页）

1 B样条曲线

1.1 B样条曲线定义

 

　　B样条方法具有表示与设计自由型曲线曲面的强大功能，是形状数学描述的主流方法之一，另外B样条方法是目前工业产品几何定义国际标准——有理B样条方法(NURBS)的基础。B样条方法兼备了Bezier方法的一切优点，包括几何不变性，仿射不变性等等，同时克服了Bezier方法中由于整体表示带来不具有局部性质的缺点（移动一个控制顶点将会影响整个曲线）。B样条曲线方程可写为：

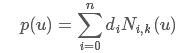
其中，d_i(i=0,1...n) 为控制顶点（坐标），N(i=0,1...n) 为 k 次规范B样条基函数，最高次数是 k。基函数是由一个称为节点矢量的非递减参数 u 的序列 U：u₀≤u₁≤...≤u_n+k+1 所决定的 k 次分段多项式。

　　B样条的基函数通常采用Cox-deBoor递推公式：

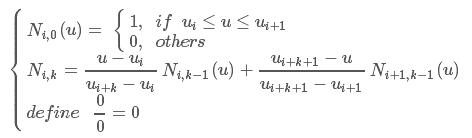
式中 i 为节点序号， k 是基函数的次数，共有 n+1个控制顶点。

注意: 区分节点和控制顶点，节点是在节点矢量 U 中取得，控制顶点则是坐标点，决定B样条的控制多边形。

Cox-deBoor递推公式是B样条曲线的定义的核心，该部分在程序中实现可采用递归的方式：

代码1：B样条基函数生成

1. % BaseFunction.m文件
2. function Nik_u = BaseFunction(i, k , u, NodeVector)
3. % 计算基函数Ni,k(u),NodeVector为节点向量
4. if k == 0 % 0次B样条
5.     if (u >= NodeVector(i+1)) && (u < NodeVector(i+2))
6.         Nik_u = 1.0;
7.     else
8.         Nik_u = 0.0;
9.     end
10. else
11.     Length1 = NodeVector(i+k+1) - NodeVector(i+1);
12.     Length2 = NodeVector(i+k+2) - NodeVector(i+2); % 支撑区间的长度
13.     if Length1 == 0.0 % 规定0/0 = 0
14.         Length1 = 1.0;
15.     end
16.     if Length2 == 0.0
17.         Length2 = 1.0;
18.     end
19.     Nik_u = (u - NodeVector(i+1)) / Length1 * BaseFunction(i, k-1, u, NodeVector) ...
20.                    + (NodeVector(i+k+2) - u) / Length2 * BaseFunction(i+1, k-1, u, NodeVector);
21. end

所给程序可用于计算基函数 N_i,k(u) 的值，程序中对不同类型的B样条曲线区别在于节点矢量 NodeVector 的取值不同。

1.2 B样条曲线的分类

　　根据节点矢量中节点的分布情况不同，可以划分 4 中类型的 B 样条曲线：

1. 均匀B样条曲线

节点矢量中节点为沿参数轴均匀或等距分布。

2. 准均匀B样条曲线

其节点矢量中两端节点具有重复度 k+1，即 u₀=u₁=...=u_k，u_n+1=u_n+2=...=u_n+k+1，所有的内节点均匀分布，具有重复度1。

3. 分段Bezier曲线

其节点矢量中两端节点的重复度与类型2相同，为 k+1。不同的是内节点重复度为 k。该类型有限制条件，控制顶点数减 1 必须等于次数的正整数倍，即: 

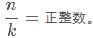
4. 一般非均匀B样条曲线

对任意分布的节点矢量 U = [u₀,u₁...u_n+k+1]，只要在数学上成立都可选取。